ChiMerge discretization algorithm
November 2, 2010
Chi merge is a simple algorithm that uses the chi-square statistic to discretize numeric attributes. It is a supervised, bottom-up data discretization method. It checks each pair of adjacent rows in order to determine if the class frequencies of the two intervals are significantly different. It tests the following hypothesis: that the two adjacent intervals are independent. If the hypothesis is confirmed the intervals are merged into a single interval, if not, they remain separated.
In this problem we select one of the following as an attribute: sepal length, sepal width, petal length, and petal width. Three Classes are available which are Iris-setosa, Iris-versicolor, Iris-virginica.
Chi merge algorithm is described below:
- Set the values for minintervals and maxintervals in order not to result in a large number or small number of intervals. Choose minintervals and maxintervals such that:
2 ≤ minintervals < maxintervals
- Look up the threshold value to use based on the significance level and the number of degrees of freedom. The threshold value can be found in statistical tables depending on two factors:
- The significance level, the higher the significance level, the higher the threshold value and the more likely the adjacent intervals will be merged.
- The number of degrees of freedom=(2-1)*([number of classes]-1) = [number of classes] -1
Here we have 3 classes thus the number of degrees of freedom is 2.
- A) Sort the attributes into ascending numerical order.
B) Create a frequency table containing one row for each distinct attribute value and one column for each class. Enter the number of occurrences of each distinct value of the attribute for each possible class in the cells of the table. Then generate a set of distinct intervals. Set the interval lower bound equal to the attribute value (inclusive) that belongs to this interval, and set its upper bound to the attribute value (exclusive) belonging to the next interval.
C) If the number of rows = minintervals then stop otherwise go to next step.
D) For each pair of adjacent rows in the frequency table calculate e the expected frequency value for that combination from the product of row and column sums divided by the total number of occurrences in the two rows combined. The expected value is the frequency value that would be expected to occur by chance given the assumption of independence. Calculate the value of (O – E) 2/E (if E<0.5, replace E by 0.5) where O is the observed frequency value for that combination, then add the values obtained to give chi 2 for that pair of adjacent rows. No chi2 is calculated for the final interval because there is not one below it.
E) Chi merge selects the smallest value of chi 2.This value is compared with a threshold, the two intervals are merged based on the following condition if chi2 is less than threshold or if the number of rows > maxintervals, if the condition is met then the two intervals are merged and the attribute for the merged row to that of the first of the two consistent rows and the upper interval bound to the upper bound interval of the next attribute. Then go to step C, but if the condition is not met then the algorithm stops.
The chi2 values are calculated for the revised frequency table, chi merge proceeds iteratively in this way merging two intervals at each stage until the chi2 for the remaining pairs of intervals are greater than the threshold value and the number of intervals is less than the maximum number of intervals, hence no further merging of intervals is possible and the discretisation is complete.
Check these ChiMerge powerpoint slides that visualizes the above algorithm.
Now lets take the IRIS data set, obtained from http://www.ics.uci.edu/~mlearn/MLRepository.html (UC-Irvine Machine Learning Data Repository), as a data set to be discretized. We will perform data discretization for each of the four numerical attributes using the Chi-Merge method having the stopping criteria be: max-interval = 6.
5.1,3.5,1.4,0.2,Iris-setosa 4.9,3.0,1.4,0.2,Iris-setosa 4.7,3.2,1.3,0.2,Iris-setosa 4.6,3.1,1.5,0.2,Iris-setosa 5.0,3.6,1.4,0.2,Iris-setosa 5.4,3.9,1.7,0.4,Iris-setosa 4.6,3.4,1.4,0.3,Iris-setosa 5.0,3.4,1.5,0.2,Iris-setosa 4.4,2.9,1.4,0.2,Iris-setosa 4.9,3.1,1.5,0.1,Iris-setosa 5.4,3.7,1.5,0.2,Iris-setosa 4.8,3.4,1.6,0.2,Iris-setosa 4.8,3.0,1.4,0.1,Iris-setosa
These attributes refer to Sepal Length, Sepal Width, Petal Length,Petal Width & Class respectively. Lets create two classes that i’ll call “IRISDataItem” and “IRISWorkItem”. The former will be used to store the attribute values for each when the data file is read while the latter will be used for later processing and storing the ChiSquare for each distinct attribute.
Public Class IrisDataItem
Public Enum IRISClass As Byte
IrisSetosa = 1
IrisVersicolour = 2
IrisVirginica = 3
End Enum
Public Property SepalLength As Single
Public Property SepalWidth As Single
Public Property PetalLength As Single
Public Property PetalWidth As Single
Public Property [Class] As IRISClass
End Class
Public Class IrisWorkItem
Public Property Attribute As Decimal
Public Property Frequency As Integer
Public Property SetosaCount As Integer
Public Property VersicolorCount As Integer
Public Property VirginicaCount As Integer
Public Property Start As Decimal
Public Property [End] As Decimal
Public Property ChiSquare As Decimal
'Operator overloading for merging of two adjacent items
Public Shared Operator ^(ByVal Item1 As IrisWorkItem, ByVal Item2 As IrisWorkItem) As IrisWorkItem
Item1.SetosaCount += Item2.SetosaCount
Item1.VirginicaCount += Item2.VirginicaCount
Item1.VersicolorCount += Item2.VersicolorCount
Item1.End = Item2.End
Item2.Frequency = -1
Return Item1
End Operator
'Operator overloading for calculating the ChiSqaure for two items
Public Shared Operator &(ByVal Item1 As IrisWorkItem, ByVal Item2 As IrisWorkItem) As Decimal
Return ChiMerge.ChiSquare(Item1, Item2)
End Operator
End Class
Our next task is to actually read the data file and fill create a List(Of IRISDataItem) object. This can be easily done by reading the file from disc, or you can embed the file in the application resources and read from there. Here is a couple of functions that handle the two ways of reading the file:
Private Function ReadDataFile(ByVal Path As String) As StringCollection
If Not String.IsNullOrWhiteSpace(Path) Then
Dim reader As New IO.StreamReader(Path)
Dim data As New StringCollection
While Not reader.EndOfStream
data.Add(reader.ReadLine)
End While
reader.Close()
Return data
Else
Throw New Exception("Invalid IRIS File Path!")
End If
End Function
Private Function ReadDataFileFromResource() As StringCollection
Dim strFile As String = System.Text.Encoding.ASCII.GetString(My.Resources.iris)
Dim reader As New IO.StringReader(strFile)
Dim data As New StringCollection
While reader.Peek > 0
data.Add(reader.ReadLine)
End While
reader.Close()
Return data
End Function
Public Shared Function CreateIrisDataItems(ByRef StringItems As StringCollection) As List(Of IrisDataItem)
If StringItems IsNot Nothing AndAlso StringItems.Count > 0 Then
Dim items As New List(Of IrisDataItem)
For Each i In StringItems
If Not String.IsNullOrWhiteSpace(i) Then
Dim item As New IrisDataItem
Dim strItem() As String = i.Split(",")
item.SepalLength = strItem(0)
item.SepalWidth = strItem(1)
item.PetalLength = strItem(2)
item.PetalWidth = strItem(3)
Select Case strItem(4)
Case "Iris-setosa"
item.Class = IrisDataItem.IRISClass.IrisSetosa
Case "Iris-versicolor"
item.Class = IrisDataItem.IRISClass.IrisVersicolour
Case "Iris-virginica"
item.Class = IrisDataItem.IRISClass.IrisVirginica
End Select
items.Add(item)
End If
Next
Return items
End If
Return Nothing
End Function
Public Shared Function CreateIrisWorkItems(ByVal AttributeIndex As Integer, ByVal DataItems As List(Of IrisDataItem)) As List(Of IrisWorkItem)
Dim workItems As New List(Of IrisWorkItem)
DataItems.ForEach(Sub(dataItem)
Dim workItem As IrisWorkItem = Nothing
Dim value As Decimal
Select Case AttributeIndex
Case 0
workItem = workItems.Find(Function(w) w.Attribute = dataItem.SepalLength)
value = dataItem.SepalLength
Case 1
workItem = workItems.Find(Function(w) w.Attribute = dataItem.SepalWidth)
value = dataItem.SepalWidth
Case 2
workItem = workItems.Find(Function(w) w.Attribute = dataItem.PetalLength)
value = dataItem.PetalLength
Case 3
workItem = workItems.Find(Function(w) w.Attribute = dataItem.PetalWidth)
value = dataItem.PetalWidth
End Select
If workItem IsNot Nothing Then
workItem.Frequency += 1
Else
workItem = New IrisWorkItem
workItem.Frequency = 1
workItems.Add(workItem)
End If
workItem.Attribute = value
Select Case dataItem.Class
Case IrisDataItem.IRISClass.IrisSetosa
workItem.SetosaCount += 1
Case IrisDataItem.IRISClass.IrisVersicolour
workItem.VersicolorCount += 1
Case IrisDataItem.IRISClass.IrisVirginica
workItem.VirginicaCount += 1
End Select
End Sub)
Return workItems.OrderBy(Function(w) w.Attribute).ToList
End Function
Having the data ready in our hands, we can now proceed to implement the ChiSquare function which is basically an implementation of the formula:
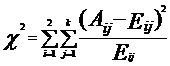
Where :
k = number of classes
Aij = number of samples in ith interval, jth class
Eij = expected frequency of Aij = (Ri * Cj) / N
Ri = number of samples in ith interval
Cj = number of samples in jth class
N = total number of samples on the two intervals
If Eij=<0.5 then set Eij to 0.5
Public Shared Function ChiSquare(ByVal Item1 As IrisWorkItem, ByVal Item2 As IrisWorkItem) As Decimal
ChiSquare = 0
Dim table(,) As Integer = {{Item1.SetosaCount, Item1.VersicolorCount, Item1.VirginicaCount}, {Item2.SetosaCount, Item2.VersicolorCount, Item2.VirginicaCount}}
Dim rowSums() As Decimal = {Item1.SetosaCount + Item1.VersicolorCount + Item1.VirginicaCount, Item2.SetosaCount + Item2.VersicolorCount + Item2.VirginicaCount}
Dim columnSums() As Decimal = {Item1.SetosaCount + Item2.SetosaCount, Item1.VersicolorCount + Item2.VersicolorCount, Item1.VirginicaCount + Item2.VirginicaCount}
Dim totalSum As Decimal = rowSums.Sum
Dim E As Decimal = 0
For i As Integer = 0 To table.GetLength(0) - 1
For j As Integer = 0 To table.GetLength(1) - 1
E = rowSums(i) * columnSums(j) / totalSum
If E > 0 Then ChiSquare += ((table(i, j) - E) ^ 2) / IIf(E < 0.5, 0.5, E)
Next
Next
End Function
One last thing to do before we implement Chi-Merge algorithm is to setup the initial interval bounds and prepare them. This is easily achieved by taking the attribute value itself to be the lower bound of the interval and the next attribute value to be the upper bound of the interval. Below is an easy way of doing this:
Public Shared Sub CreateIntervalBounds(ByVal Items As List(Of IrisWorkItem))
For i As Integer = 0 To Items.Count - 2
Items(i).Start = Items(i).Attribute
Items(i).End = Items(i + 1).Attribute
Next
Items(Items.Count - 1).Start = Items(Items.Count - 1).Attribute
Items(Items.Count - 1).End = Items(Items.Count - 1).Attribute + 1
End Sub
Finally, we are ready to implement the Chi-Merge algorithm. One thing to note about the below implementation is the use of LINQ to Objects and Lambda Expressions to filter out tuples that need to be dropped and merged. So you could probably that the code below will compile only using Visual Studio 2010 and .Net Framework 4.0. I haven’t tested it on Visual Studio 2008 Sp1 but if you do let me know if it compiles well.
Public Sub Compute(ByRef Items As List(Of IrisWorkItem))
For i As Integer = 0 To Items.Count - 2
Items(i).ChiSquare = Items(i) & Items(i + 1) 'calculate chiSquare
Next
Dim minChiSquare As Decimal = Items.Take(Items.Count - 1).Min(Function(x) x.ChiSquare)
If minChiSquare < THRESHOLD Then
Dim i As Integer = 0
While i < Items.Count
If Items(i).ChiSquare = minChiSquare Then
Items(i) ^= Items(i + 1) 'merge
Dim j As Integer = i
i += 1
While i < Items.Count - 1 AndAlso Items(i).ChiSquare = minChiSquare
Items(j) ^= Items(i + 1) 'merge
i += 1
End While
End If
i += 1
End While
Items.RemoveAll(Function(x) x.Frequency = -1)
If Items.Count >= MIN_INTERVAL Then Compute(Items)
Else
If Items.Count > MAX_INTERVAL Then
THRESHOLD += 0.5
Compute(Items)
End If
End If
End Sub
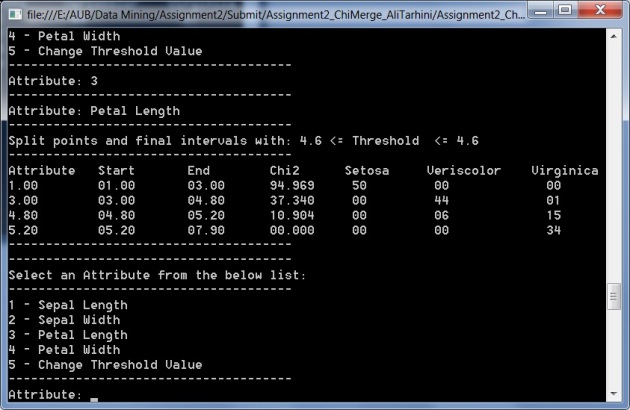
Once you run the algorithm, you can compare the obtained intervals and split points with the ones found on the internet. Below are my final results compared to the results on http://sci2s.ugr.es/keel/pdf/algorithm/congreso/1992-Kerber-ChimErge-AAAI92.pdf
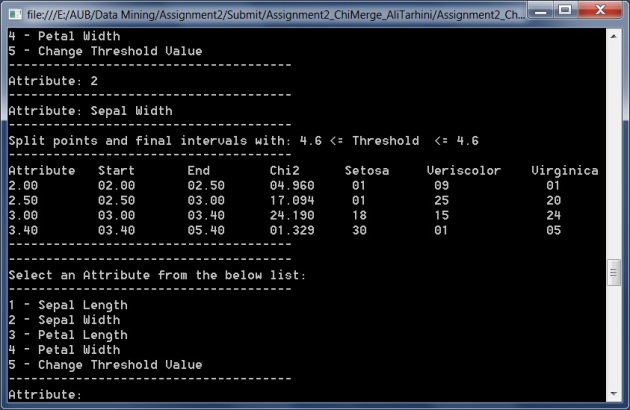
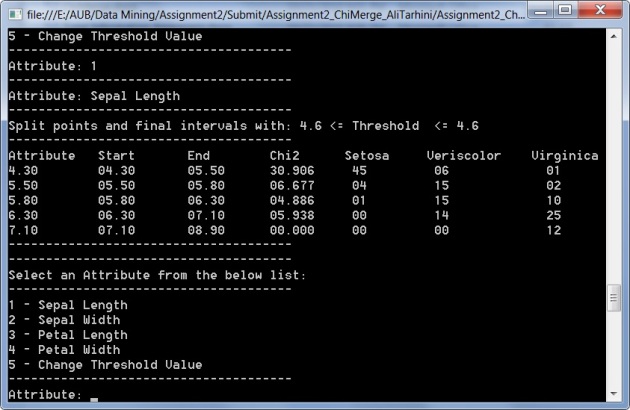
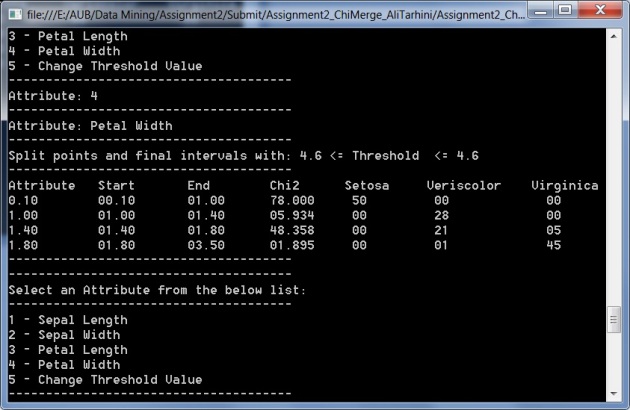
 Welcome to Ali's blog, A computer engineer & scientist specialized in software development and algorithms.
Welcome to Ali's blog, A computer engineer & scientist specialized in software development and algorithms.
You must be logged in to post a comment.